【微评】黄金是资产配置中最重要的砝码
市场上可供投资的资产种类繁多,如股票、基金、P2P、黄金、房地产、艺术品、银行理财产品等,各类投资品种的风险水平、期望收益、产品特性有所不同。在投资过程中应选择哪几种资产进行配置以及如何确定不同资产中之间的投资比例是一个值得深思的问题。

通过观察近二十年黄金价格与GDP增长走势,如图1。在经济萧条时期,特别是在今年疫情影响下,全球经济衰退,而金价却不断上涨。从图2中可以发现,在通胀率比较高的情况下,黄金也会出现与CPI相同的走势,二者之见表现出“同升同降”的趋势。根据黄金价格与CPI的这种关系,在出现高通胀或者利率较低时,黄金能够很好地起到保值增值的作用。
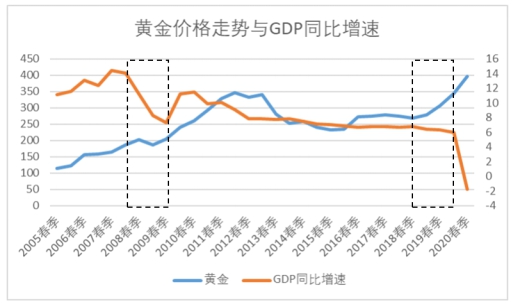
图1 黄金价格(元/克)与GDP增速(%)
注:数据来源于Choice金融数据库;年份:2005年春-2020年春
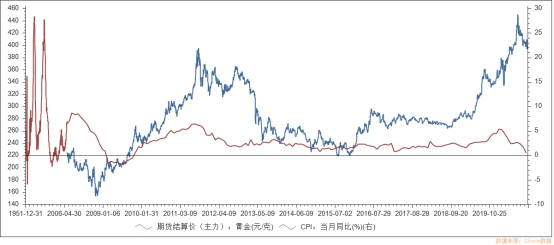
图2 同期黄金期货价格(元/克)与CPI(%)
注:数据来源于Choice金融数据库;年份1951年12月-2020年10月
另一方面,黄金和其他资产的相关性较低,对于投资者来说应该追求在给定风险水平下获得更高的预期收益。根据马科维茨的资产组合理论,在组合中加入相关性低的资产能够起到分散风险的作用,推动有效边界向左上方移动,进而优化投资组合。特别是,在今年新冠疫情影响下,黄金价格持续走高,充分展现出其避险资产的功效。

因此长期以来,黄金主要被人们当作对抗通胀和避险的资产,而非从投资的角度考虑黄金资产配置。集货币属性非货币属性、金融属性商品属性于一身的黄金,难道它在资产配置中仅用于避险、抗通胀功能吗?本文把资产配置与黄金联系起来,基于国内股票、国外股票、和房地产,采用2005-2019年数据,通过描绘不同投资组合的有效边界,研究在不考虑杠杆情况下,黄金在资产配置中的重要意义。
一、文献综述
蒋先玲,王炳楠(2017)选用了不同起点到2017年5月的不同指标的月度数据进行平稳性检验、协整检验、格兰杰因果检验,研究国际黄金的波动特征与影响因素。研究发现,在长周期下,黄金价格周期与经济发展同期相反;中周期表现出与大宗商品的价格周期相一致的特征;短周期内黄金价格受到突发因素影响较大。

Jaffe, Jeffrey F(1989)基于1971年到1987年数据,发现在四种同成分不同比例的投资组合中分别加入5%和10%的黄金,发现投资组合的回报率提高,同时风险降低。Thi-Hong-Van Hoang, Hooi Hooi Lean, Wing-Keung Wong(2015)基于1949年到2012年数据,采用随机优势法,评估1949年至2012年巴黎黄金报价在法国投资组合多元化中的作用,研究发现,在股票投资组合中包含黄金, 可以改善投资组合,而如果把黄金纳入无风险投资组合,没有任何优势。王光伟,潘轶民(2005)基于2001年世界黄金委员会发布的公共政策研究报告,发现:加入黄金和加入债券都可以减少资产组合波动性,而黄金能够更好分散风险;加入黄金和加入债券都能减少厚尾和偏度的产生,从而使收益率更接近正态分布,而黄金效果更好。
杨柳勇,史震涛(2004)通过模型模拟结果,发现国际金价与道琼斯工业指数存在强烈负相关,与通货膨胀率正相关,与美元指数和利率水平负相关。王光伟,潘轶民(2005)提到,黄金和标普500指数从长期来看,没有显著相关性而呈现略微负相关,且当市场出现动荡时,黄金与其他资产会呈现显著负相关/Eric J.Levin,Robert E.Wright(2006)研究黄金价格决定因素,研究发现,黄金价格和美国消费者指数存在显著正相关,在长经济周期内,黄金可以作为抵御通货膨胀风险的工具。Jaffe, Jeffrey F(1989)发现,黄金和其他资产(标普500指数、小公司股票、长期政府债券、国库券等资产)的相关性较低,和外汇存在负相关,与CPI正相关。
二、研究方法与数据
(一)研究方法
均值方差模型是由哈里·马科维茨 (H. M. Markowitz) 在1952年提出的风险投资模型。马科维茨把资产的期望收益率定为资产的收益指标,把收益率的波动(标准差)定为资产的风险指标,为投资组合分析提供重要的理论基础和实际可操作的分析框架体系。

均值方差模型基于一系列假设:(1)投资者的决定仅仅基于风险和收益;(2)投资者使用标准差来衡量风险;(3)投资者在考虑每一次投资选择时,其依据是某一持仓时间内的证券收益的概率分布。故而投资者进行资产选择,在收益率相同时,会选择标准差更小的资产组合,在标准差相同时,会选择收益率更高的投资组合。
本文基于均值方差模型,使用Python,基于蒙特卡罗模拟法进行有效边界的构建,具体步骤如下:(1)计算各资产的年化收益率和年化标准差,并算出协方差矩阵;(2)在0到1的均匀分布上随机取出一组数,并令其和为1,作为各资产比例;(3)计算资产组合的组合收益率和组合标准差;(4)将以上步骤重复进行30万次,得到30万组不同资产比例的资产组合;(5)在同收益率水平上,取出标准差最小的组合;(6)在同标准差时,取出收益率最高的组合,该组合即为有效边界,画出有效边界。
(二)数据来源与选取

总共讨论4个资产构成的资产组合,分别是黄金、房地产、国内股票,国外股票,时间从2005年为开始,到2019年结束,数据来源于Choice金融数据库。
黄金选择上海黄金交易所中的黄金Au9995,Au9995即是纯度99.95的黄金,具有充足流通量,其价格变化具有代表性。房地产价格选择我国商品房销售额除以商品房销售面积,以我国商品房平均价格代表房地产价格走势。国内股票、国外股票数据来自于Choice金融数据库,国内股票选择沪深300指数,国外股票选择道琼斯指数。

三、研究结果:黄金在资产配置中的作用
(一)与其他资产的相关性分析
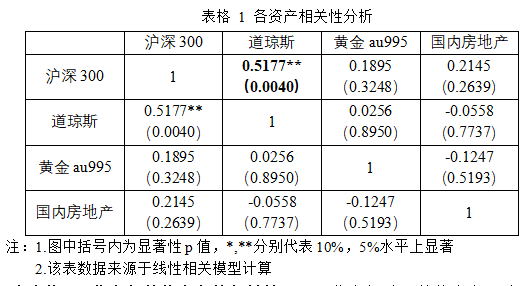
由表格1,黄金和其他资产的相关性更弱。黄金相对于其他资产,除了商品属性,还具有货币属性,这是其他资产并不具备的。即马克思在《资本论》中所说“金银天然不是货币,但货币天然是金银。”,马克思看到了黄金的金融属性,但他强调的黄金天然不是货币往往被人忽视,这是强调黄金的物理属性、商品属性和非货币化属性。而黄金的价格波动正是因为不同属性的交替波动,商品属性帮助投资者规避通胀风险,货币属性又能帮助投资者规避宏观层面系统性风险。
(二)资产组合中加入黄金的作用
以沪深300指数、道琼斯指数、房地产为底层资产,往资产组合中加入黄金,画出资产组合可行域,即同收益率,取标准差最小的资产组合,并保留下有效边界,即同标准差,保证收益率最大。

图3在三资产组合中加入黄金
注:该图来自于Python程序,曲线为有效边界,左边曲线为加入黄金后有效边界
数据来源:Choice金融数据库,国内股票选择沪深300指数,国外股票选择道琼斯指数;年份:2005年-2019年
由图3可以看到,黄金的加入,让组合的有效边界向左上角移动。例如,在收益率同为8.5%的情况下,加入黄金的资产组合位于C点,而未加入黄金的资产组合位于B点,C点组合标准差更低,意味着在预期收益率相同时,黄金的加入降低了组合的波动;在标准差相同情况下,加入黄金的资产组合位于A点,而未加入黄金的资产组合位于B点,A点组合收益率更高,意味着在风险一致情况下,黄金的加入使得提高了组合的预期收益率。
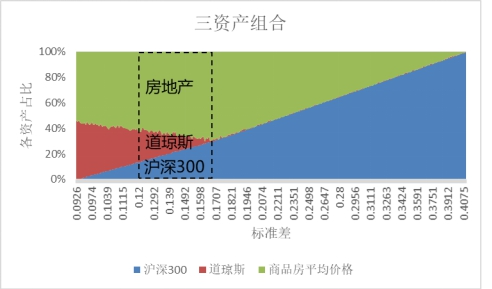
图4-1 资产组合有效边界各资产占比比较:未加入黄金
图4-2资产组合有效边界各资产占比比较:加入黄金
注:图中标签顺序自下而上,最下方资产为沪深300
数据来源:Choice金融数据库,国内股票选择沪深300指数,国外股票选择道琼斯指数;年份:2005年-2019年
当黄金加入资产配置后,有效边界中黄金主要替代了道琼斯指数,占相当大部分,这显示了黄金在资产配置中的重要地位。图4-2是在加入黄金之后,资产组合有效边界资产占比的变化,横轴为标准差,意味着在标准差不同情况下,有效边界中各资产占比。在加入黄金之前,资产组合有效边界中,各资产占比主要由沪深300指数和房地产组成,道琼斯只占少数比例。
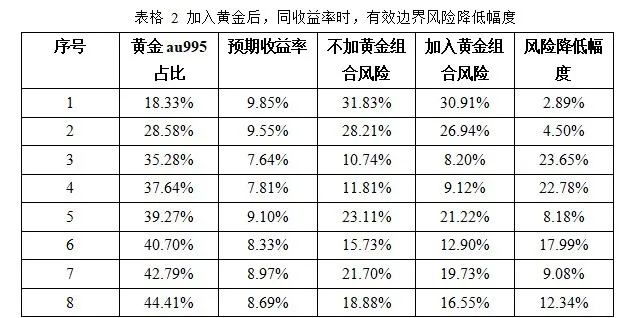
资产组合中加入黄金可以有效降低组合风险。表格2是在资产组合中加入黄金,和未加入黄金的比较。在相同预期收益率下,比较有效边界上风险资产组合的风险。一方面,加入黄金可以极大改善投资组合,起到降低资产组合风险的作用,且在黄金占比为35.28%时,降低风险幅度为23.65%;另一方面,可以具体看到黄金在有效边界中的占比,在加入黄金的有效边界中,黄金普遍占比较大,且随着黄金占比的增加,风险降低幅度并没有出现有规律的变化。
四、研究结论
(一)基于均值方差模型,从投资角度来看,在期望收益率不变的情况下,适当比例黄金的加入,在很大程度上能够降低投资组合风险。
(二)黄金与其他金融产品的不同之处在于所有权与使用权未分离,在追求较高预期收益率时,黄金的加入对投资组合的优化效果不显著。
五、总结
对于偏好低风险投资者,持有适当比例的黄金是资产配置的明智选择。如果在各个微观主体的投资组合中加大黄金投资比例,从宏观意义上来看还会对维护国家金融安全增添助力。“美元涨黄金跌,美元跌黄金涨”反应了供求规律。但事实证明,黄金在历次美元量化宽松节点上,黄金价格不涨反跌。是因为美元对美国垄断财阀的利益远远超过黄金,通过手中持有的黄金定价权打压黄金价格保障美元在全球的利益。黄金储备是一国金融安全最后的守门员,而我国黄金储备量相对较低。因此“藏金于民”是既有益于微观投资者,又有助于增强我国金融安全的一剂良方。
(此文发表于新华财经)
本文作者为景乃权,浙江省公共政策研究院研究员;刘学辉、丁瀚、郑斌武、贺嘉豪、张洵、严雨沁,浙江大学金融系研究生,感谢大力支持!